【LuoguP2580】于是他错误的点名开始了
题目链接: https://www.luogu.org/problemnew/show/P2580
前言
这篇题解原来是我放到Luogu上的,打算搬过来,原地址: https://ciyang.blog.luogu.org/solution-p2580
当时是自己闲得无聊自创的算法,跑了最优解第3,Trie树中最快了
不过后来Luogu上的dalao告诉我这个是边压Trie树,因此人生失去意义
此题解非正常字典树,推荐先学习普通的字典树并了解指针的使用
代码还是之前的代码,名为Lumpy_Tnode.
简介
树上的边存储字符串,代表节点的单独前缀.
写题解的上午有了灵感,然后根据思路模拟了一下,可行性挺高的.代码上比普通的复杂一些,我使用了指针.
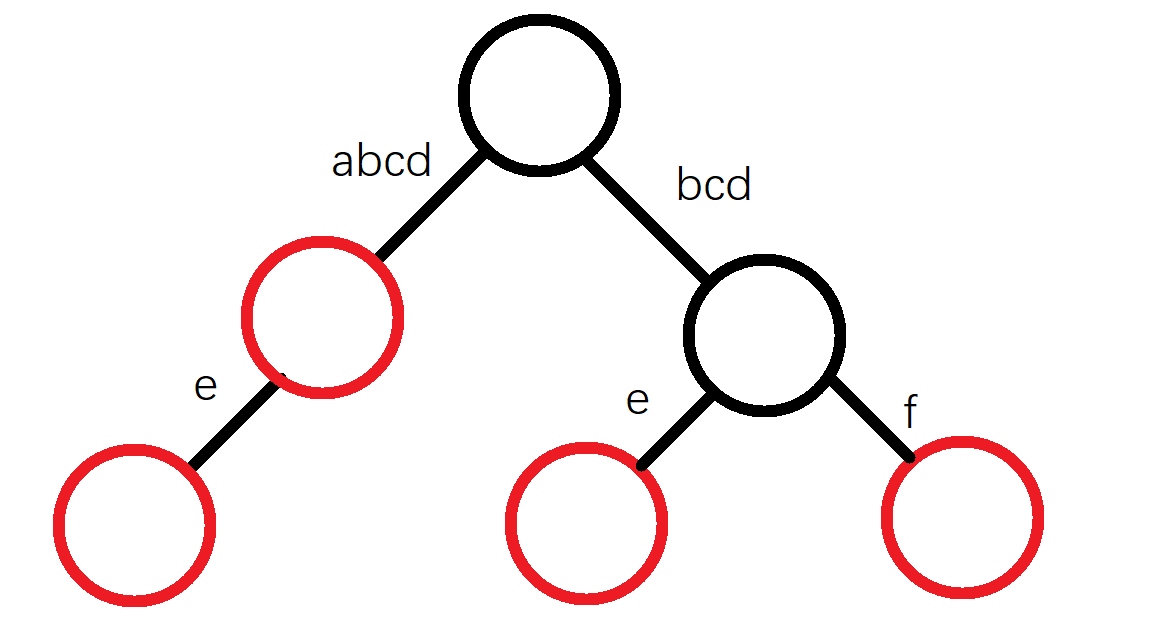
按任意顺序插入abcd,abcde,bcde,bcdf四个字符串的Trie树长这样
红色节点表示已插入字符串的结尾节点
证明
通过与比较普通指针版和非指针版Trie来证明一下可行性.
已知一个节点要保存26条边的指针
指针版Trie可使用动态内存,缺点是每个节点只保存一个字符,会有大量边的空指针来占用额外的内存,且new节点多了,内存分配常数较大.
为了减少常数,可以自己写内存池分配,但无论是什么数据,只要稍带随机性形成链,就会有很多只有一个子节点的节点,这无疑有25个空指针浪费内存.
非指针版常数小,但空间分配也是很大的问题,多了可能MLE,少了RE.然而仍有很多一条链的树,空间最大浪费N*25啊…先不说影响美观而且时间复杂度依然很高,毕竟查询也是O(N).
边压Trie的复杂度是会改变的,就是对一条链情况的优化,理论最大时间复杂度是O(N)带有一些常数,不考虑常数情况下,永远小于等于普通Trie.
边压Trie巧妙利用字符串指针,赋值、继承等操作只需要指针或长度变化就好了,因此插入最小复杂度是O(1),空间上也少了很多空指针.
太多证明不如一句代码,我放上代码继续分析.
解析
节点的结构体,原来的char变成了length和字符串指针:
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
| #define clear(a) memset(a, 0, sizeof(a))
#define copy(a, b) memcpy(a, b, sizeof(a))
struct Lumpy_Tnode {
const char *pStr;
int length, isEnd;
Lumpy_Tnode *children[26];
inline Lumpy_Tnode() {
pStr= 0, length= isEnd= 0, clear(children);
}
inline Lumpy_Tnode(const char *str, int len, int end) {
pStr= str, length= len, isEnd= end, clear(children);
}
} mNode;
|
插入操作
使用递归和循环,判断比较多,先看代码(看起来常数很大)
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
| inline void insert(const char *str, int length, Lumpy_Tnode *bNode) {
if(!length) {
bNode->isEnd= 1;
return;
}
int ch= str[0] - 'a';
if(bNode->children[ch]) {
bNode= bNode->children[ch];
register int sptr= 0;
while(sptr < length && sptr < bNode->length && bNode->pStr[sptr] == str[sptr]) ++sptr;
if(sptr != bNode->length) {
Lumpy_Tnode *nNode= new Lumpy_Tnode(bNode->pStr + sptr, bNode->length - sptr, bNode->isEnd);
copy(nNode->children, bNode->children), clear(bNode->children);
bNode->isEnd= 0, bNode->children[bNode->pStr[sptr] - 'a']= nNode;
}
bNode->length= sptr;
insert(str + sptr, length - sptr, bNode);
}
else
bNode->children[ch]= new Lumpy_Tnode(str, length, 1);
return;
}
|
如果代码看懂了,第一反应可能认为指针操作有一些漏洞.
的确插入的字符串在插入后就不能进行改变了,所以就只要开一个char[N][K]的数组来保存输入的字符串,K为最长字符串的长度.
相比较空间复杂度总体仍然较小,其实是把原来每个节点存的char放到了一起,每个节点多了一个指针.
这其中其实有个很巧妙的事,树上的一条链可能指向的地址是连续的.仔细想了想,其实也有空间浪费,不管是节点上还是树上的最长公共前缀都只指向一个字符串,其他字符串中相同的字符占用的空间就浪费掉了,这句话不懂没事,因为这个浪费造成的影响很小.
如果代码都没看懂,还有图解:
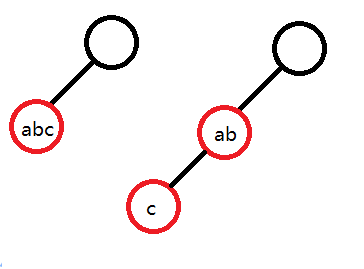
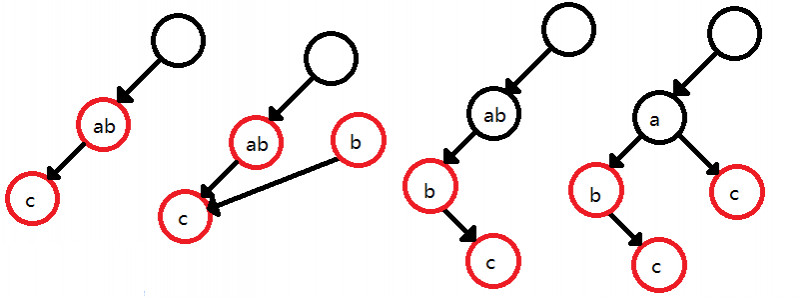
解释一下图2:
比较ab和ac,最长公共前缀为a
新建一个字符串指针指向ab中b的节点,长度为1,继承ab的颜色和ab的子节点.
清空ab的子节点,颜色改为黑(黑表示不为结尾节点),ab的首字母b子节点指向b.
在我实现时,先更改长度使ab变为a,再向a中插入c.
因为没有首字母为c的子节点,直接new一个新的.
查找操作
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
| inline int find(const char *str, int length, Lumpy_Tnode *bNode) {
if(!length) {
if(bNode->isEnd == 1) return bNode->isEnd++;
return bNode->isEnd;
}
int ch= str[0] - 'a';
if(bNode->children[ch]) {
bNode= bNode->children[ch];
if(length < bNode->length) return 0;
register int sptr= 0;
while(sptr < bNode->length && bNode->pStr[sptr] == str[sptr]) ++sptr;
if(sptr != bNode->length) return 0;
return find(str + sptr, length - sptr, bNode);
}
return 0;
}
|
比插入的代码简单多了,并且自带剪枝,所以比较快.
代码
(开启O2) 用时: 127ms / 内存: 4248KB
(关闭O2) 用时: 144ms / 内存: 4128KB
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
| #include <iostream>
#include <stdio.h>
#include <string.h>
using namespace std;
#define clear(a) memset(a, 0, sizeof(a))
#define copy(a, b) memcpy(a, b, sizeof(a))
struct Lumpy_Trie {
struct Lumpy_Tnode {
const char *pStr;
int length, isEnd;
Lumpy_Tnode *children[26];
inline Lumpy_Tnode() {
pStr= 0, length= isEnd= 0, clear(children);
}
inline Lumpy_Tnode(const char *str, int len, int end) {
pStr= str, length= len, isEnd= end, clear(children);
}
} mNode;
inline void insert(const char *str, int length, Lumpy_Tnode *bNode) {
if(!length) {
bNode->isEnd= 1;
return;
}
int ch= str[0] - 'a';
if(bNode->children[ch]) {
bNode= bNode->children[ch];
register int sptr= 0;
while(sptr < length && sptr < bNode->length && bNode->pStr[sptr] == str[sptr]) ++sptr;
if(sptr != bNode->length) {
Lumpy_Tnode *nNode= new Lumpy_Tnode(bNode->pStr + sptr, bNode->length - sptr, bNode->isEnd);
copy(nNode->children, bNode->children), clear(bNode->children);
bNode->isEnd= 0, bNode->children[bNode->pStr[sptr] - 'a']= nNode;
}
bNode->length= sptr;
insert(str + sptr, length - sptr, bNode);
}
else
bNode->children[ch]= new Lumpy_Tnode(str, length, 1);
return;
}
inline int find(const char *str, int length, Lumpy_Tnode *bNode) {
if(length == 0) {
if(bNode->isEnd == 1) return bNode->isEnd++;
return bNode->isEnd;
}
int ch= str[0] - 'a';
if(bNode->children[ch]) {
bNode= bNode->children[ch];
if(length < bNode->length) return 0;
register int sptr= 0;
while(sptr < bNode->length && bNode->pStr[sptr] == str[sptr]) ++sptr;
if(sptr != bNode->length) return 0;
return find(str + sptr, length - sptr, bNode);
}
return 0;
}
} t;
char allstr[10001][51], tmp[51];
int n;
int main() {
scanf("%d", &n);
for(register int i= 0; i < n; i++) {
scanf("%s", allstr[i]);
t.insert(allstr[i], strlen(allstr[i]), &t.mNode);
}
scanf("%d", &n);
for(register int i= 0, j; i < n; i++) {
scanf("%s", tmp);
j= t.find(tmp, strlen(tmp), &t.mNode);
switch(j) {
case 0: printf("WRONG\n"); break;
case 1: printf("OK\n"); break;
case 2: printf("REPEAT\n"); break;
}
}
return 0;
}
|
最需要注意的是输入的字符串insert后不能再更改那一块内存了不能更改了…
后续
我写的常数可能挺大,希望dalao们试试各种卡常优化…



